728x90
Tree
Tree 개념, 주요 용어
Tree의 개념
- 노드와 링크를 이용한 자료구조
- 족보 구조
- 트리 구조로 많은 알고리즘을 구현하는 이유 :
- 다른 자료구조보다 자료를 저장하거나 검색하는 등의 방법이 간단하고 메모리를 효율적으로 사용 가능
트리 관련 주요 용어
선택한 요소의 '마지막'에 새로운 요소나 콘텐츠를 추가
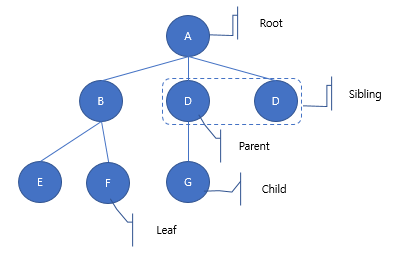
ㅇ노드의 주요 용어
| 용어 | 설명 |
|---|---|
| 루트 노드, Root Node | 연결된 노드가 한 군데로 모이는 상위에 위치하는 노드 (노드 A) |
| 차수, Degree | - 한 노드에 연결된 서브 트리의 개수 -차수가 2개 이하인 트리 구조를 이진 트리(Binary Tree)라고 부른다. - 노드 A의 차수는 노드 A에 연결된 서브 트리가 모두 3개이므로 3이 되고, 노드 B의 차수는 노드 B에 연결된 노드가 2개이므로 2 |
| 부모 노드, Parent Node | - 현재의 노드에 연결되어 있는 바로 상위 노드 - 트리 구조에서는 루트 노드를 제외하고는 모든 노드가 하나의 부모 노드를 가져야 한다. - 부모 노드가 2개 이상 존재하면 그 구조는 트리 노드가 될 수 없다. |
| 자식 노드, Child Node | - 부모 노드의 반대 개념 자신보다 아래에 있는 노드를 자식 노드라고 한다 - 트리 구조에서 이진 노드는 반드시 자식 노드의 개수가 2개 이하가 되어야 한다 |
| 형제 노드, Sibling Node | 같은 부모 노드를 갖는 노드 사이 |
| 리프 노드, Leaf Node | 가장 끝에 있는 최하위 노드 - 단말 혹은 터미널(Terminal) 노드라고도 한다. |
| 레벨, Level | - 레벨은 루트 노드부터 해당 노드까지 경로를 찾는데 방문한 총 노드의 수 - 루트 노드를 레벨 1로 하여 한 단계씩 내려올 때마다 레벨이 1씩 증가. |
| 높이(Height) or 깊이(Depth) | 트리의 최대 레벨 수를 트리의 높이 혹은 트리의 깊이라고 한다. |
이진 트리
- 자식 노드를 2개 이하만 갖는 트리
- 트리의 차수 Degree가 2 이하인 트리를 의미
- 자식 노드가 2개만 존재하므로 구현이 쉽다
이진 트리의 노드 정의
C
typedef struct _NODE {
char data;
struct _NODE *left;
struct _NDOE *right;
} NODE;
Java
class Node {
char data;
Node left;
Node right;
public Node(char data) {
this.data = data;
this.left = null;
this.right = null;
}
}
JavaScript
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
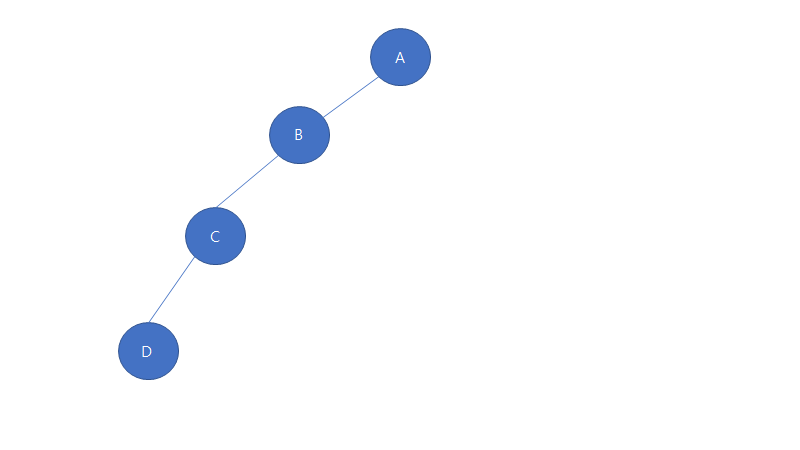
왼쪽으로 기울어진 이진 트리
리프 노드를 제외하고 모든 노드가 왼쪽으로 자식 노드만 갖는 트리
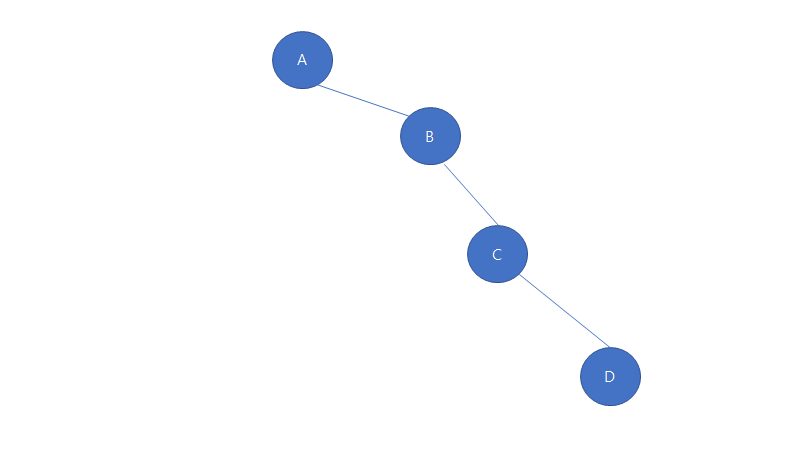
오른쪽으로 기울어진 이진 트리
마지막 리프 노드를 제외하고 모든 노드가 오른쪽 자식 노드만을 갖는 트리
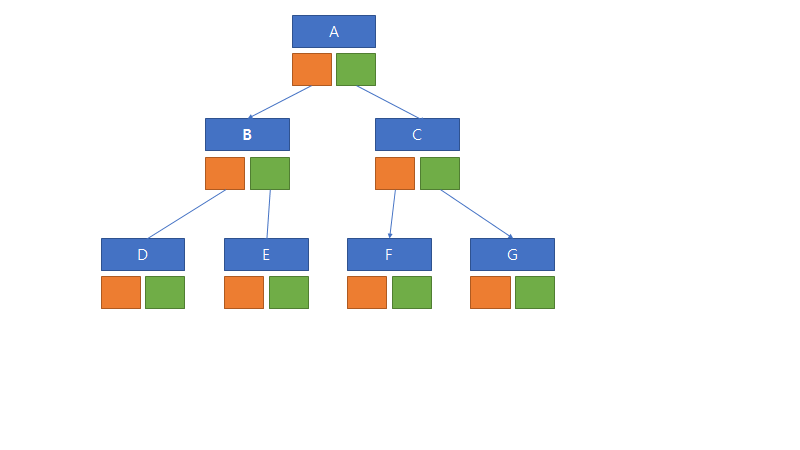
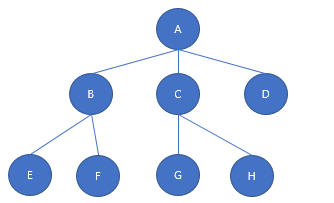
완전 이진 트리
모든 노드에 자식 노드가 하나도 없거나 아니면 2개의 자식 노드를 갖는 이진 트리
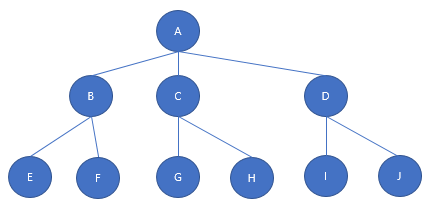
정 이진 트리
리프 노드들의 레벨이 같아야 하는 트리.
앞의 완전 이진 트리와는 다르게 각각의 B, C, D의 자식 노드까지 향하는 레벨이 각각 3으로 같다.
트리의 순회 알고리즘
순회 Traverse : 트리 구조에서 각각의 노드를 방문하는 것
- 전위 순회, Pre-Order Traverse
- 중위 순회, In-Order Traverse
- 후위 순회, Post-Order Traverse
- 단계 순회, Level-Order Traverse
'Algorithm > basic' 카테고리의 다른 글
| 알고리즘 기초 6 - [자료구조, 덱] (0) | 2021.03.09 |
|---|---|
| 알고리즘 기초 5 - [자료구조, 큐] (0) | 2021.03.09 |
| 알고리즘 기초 4- [자료구조, 스택] (0) | 2021.03.08 |
| 알고리즘 기초 3 - [자료구조, 이중링크드리스트, 삽입(검색), 삭제(검색)] (0) | 2021.03.08 |
| 알고리즘 기초 2 - [자료구조, 단일링크드리스트(삽입, 삭제, 검색)] (0) | 2021.03.08 |